Planetary Science

Orbital mechanics #

Orbital parameters #

• Orbital period
• Inclination
• Eccentricity

Simulators #

Heliocentric orbital simulator: https://ssd.jpl.nasa.gov/tools/orbit_diagram.html

Specific simulator for Saturn: https://gravitysimulator.org/solar-system/saturn-and-its-rings-and-major-moons

Rotation parameters #

• Rotation period
• Axial tilt

Celestial coordinates #

• Ascension
• Declination

Gravitational resonance #

Trojan satellites #

Planetary features #

Spectrum #

Albedo #

Peaks of eternal light #

https://en.wikipedia.org/wiki/Peak_of_eternal_light

Permanently shadowed craters #

https://en.wikipedia.org/wiki/Permanently_shadowed_crater

Planetary Topography #

Spheroid #

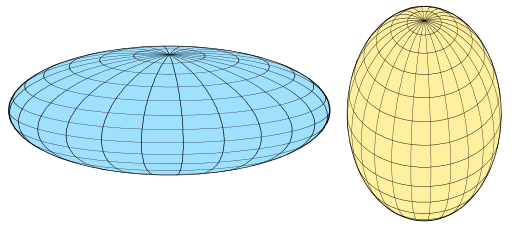
Oblate and prolate spheroids. Source.

A spheroid, also known as an ellipsoid of revolution or rotational ellipsoid, is the surface obtained by rotating an ellipse about one of its principal axes; in other words, an ellipsoid with two equal semi-diameters. A spheroid has circular symmetry.

If the ellipse is rotated about its major axis, the result is a prolate spheroid, elongated like a rugby ball.

If the ellipse is rotated about its minor axis, the result is an oblate spheroid, flattened like a lentil or a plain M&M.

If the generating ellipse is a circle, the result is a sphere.

Due to the combined effects of gravity and rotation, planets are not quite in the shape of a sphere, but instead is slightly flattened in the direction of their axis of rotation.

Quadrangles #

TDB

Distance of the horizon #

Distance to the true horizon from an observer close to the planet’s surface is about \(d \simeq \sqrt{2 h R}\) where h is height above sea level and R is the radius. For instance:

• On Earth, in standard atmospheric conditions, for an observer with eye level above sea level by 1.70 metres, the horizon is at a distance of about 5 km.

• On Mars, where R = 3300km, for the same observer the horizon would be at \(d \simeq \sqrt{2*1.7m*3300000m} \simeq 3.5\) km

• On Europa, where R = 1561km, for the same observer the horizon would be at \(d \simeq \sqrt{2*1.7m*1561000m} \simeq 2.3\) km

Calculator #

Insert the height of the observer and the radius of the planet to obtain the horizon distance, calculated with the formula above.

Planetary Geology #

Cold trap #

https://en.wikipedia.org/wiki/Cold_trap_(astronomy)

Solar System #

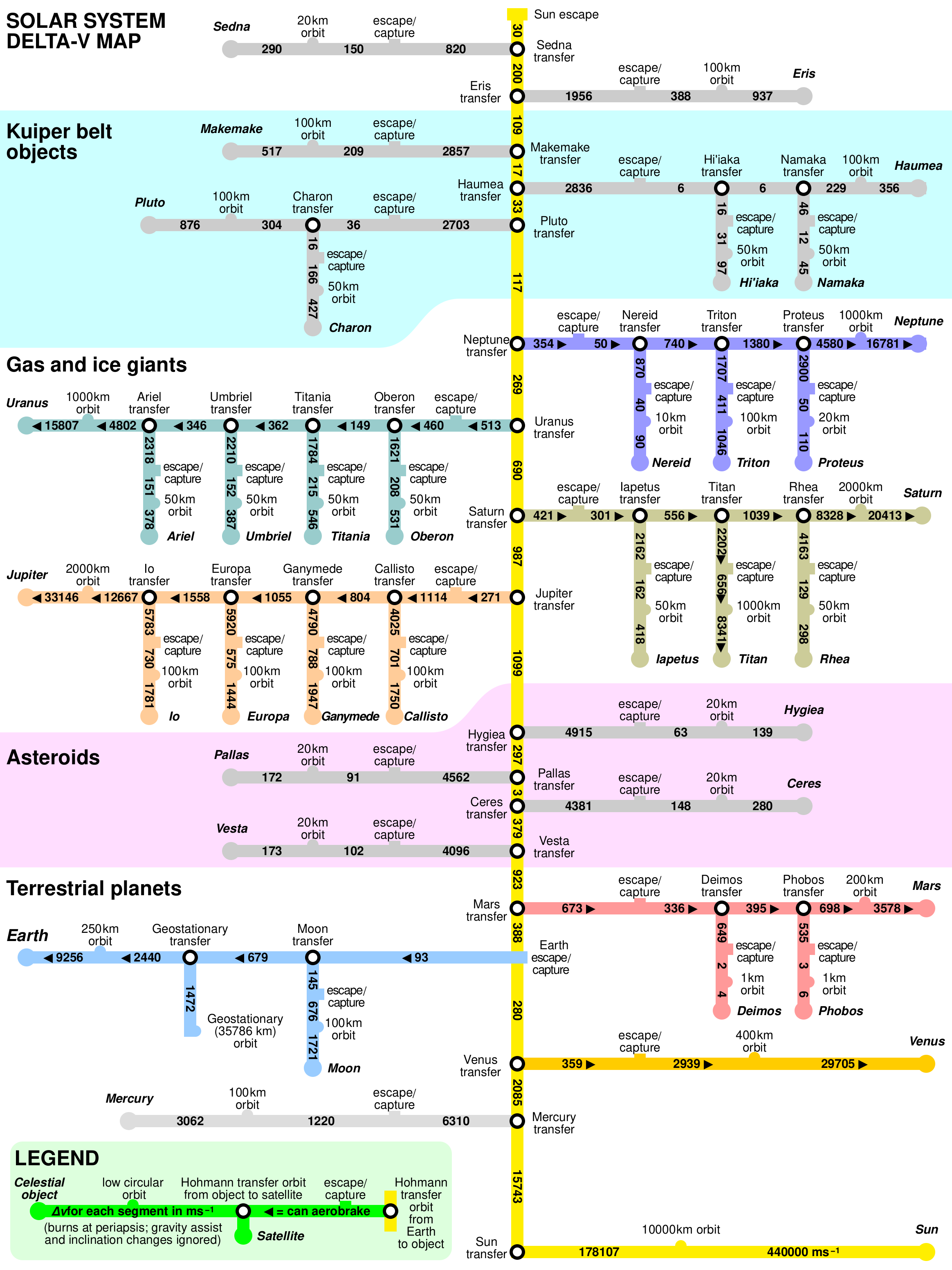
Delta-v requirements for main Solar System bodies #

Coordinates system #

Ecliptic coordinate system #

This spherical coordinate system is uses to specify the position of various orbiting bodies with respect to the Sun [1].

Such coordinate system can also be centered on a specific planet to define the orbits of its moons or satellites, as it’s sometimes done with the Earth.

The name of the coordinates are:

• If heliocentric (centered on the Sun):

  • longitude: l
  • latitude: b
  • distance: r

• If geocentric (centered on the Earth or another planet with orbiting satellites):

  • longitude: λ (lowercase lamda)
  • latitudine: β (lowercase beta)
  • distanza: Δ (uppercase delta)

References #

[1] “Ecliptic_coordinate_system” https://en.wikipedia.org/wiki/Ecliptic_coordinate_system.